During the Baksan School, each team will complete one scientific project. Projects are offered in two styles, accommodating your different interests and strengths:
Innovative projects
For those who enjoy creative thinking, inventing novel detection
methods, and proposing bold new scientific ideas
Calculation-focused projects
For those who prefer detailed analytical work,
performing rigorous estimations, simulations, and quantitative analysis
Your Tasks Include
- Clearly defining the scientific goals of your project
- Working out details (conceptually or mathematically) and creating plots and animations, if necessary, to illustrate the results and ideas
- Preparing a short scientific report in LaTeX (4-5 pages)
- Presenting your results in a concise and engaging talk (10 min)
The details and specific goals of each project are provided individually.
Please, subscribe to a preferred project by using this form (max 10 people).
Enjoy collaborating, be curious, and have fun!
Here you can find a description of each project. You can find this information also in this document.
Project 1. One Neutrino to Bring Them All. What Can We Learn from the KM3NeT Extreme-Energy Event?
In February 2025, Nature published the observation of a neutrino with a record energy of 220 PeV by the KM3NeT experiment. At the same time, the IceCube experiment – with a significantly larger effective volume and exposure – has not reported any neutrinos with such high energies. What conclusions can be drawn about the nature of neutrino sources based on a single extreme-energy detection?
Tasks:
- Create a digital model of the neutrino flux and its registration by two experiments: IceCube and KM3NeT
- Model the effective areas, exposures, and energy resolutions of both detectors
- Implement various source scenarios: isotropic extragalactic flux, Galactic sources, radio blazars, and other models from literature
- Using the digital model, calculate the probability that KM3NeT will detect a neutrino with energy >100~PeV before IceCube, for different source types
- Compare the outcome across multiple scenarios
- Identify which models are more consistent with the observed event
- Discuss which source model (if any) is preferred under this assumption
- Assume the event is real and published by KM3NeT
- What flux would KM3NeT have to infer from this single event?
- Compare this “published” flux to the one assumed in the model
- Analyze the tension/consistency between assumed source properties and inferred flux
- Estimate the detection probabilities analytically and compare with numerical result
- Estimate the event probability analytically (using e.g. Poisson/Exp. distribution)
- Compare the analytical estimate with the model predictions to verify or interpret them
Deliverables:
- Code and Plots: digital model implementation, simulated event rates, and comparisons between IceCube and KM3NeT across scenarios
- Scientific Report: a concise LaTeX-written report summarizing assumptions, modeling methods, results, and conclusions
- Presentation: a 10-minute talk presenting your findings, including interpretation of the KM3NeT detection, model preference, and implications for future observations
Project 2. Cosmological evolution from FRBs
Fast Radio Bursts (FRBs) are a recently discovered astrophysical phenomenon (2007), with over 1000 events detected to date. For more than 100 of them, the redshift is measured.
These events provide a unique opportunity to probe the large-scale structure and evolution of the Universe.
Tasks:
- FRB Catalog Construction: Compile a catalog of observed FRBs, including dispersion measure (DM), sky position, observed flux, pulse width (if available). Add redshifts, if available
- Population Modeling and Inference
- Construct a model for the spatial and redshift distribution of FRBs
- Use Markov Chain Monte Carlo (MCMC) to explore the parameter space and infer best-fitting values and uncertainties using the catalog without redshifts
- Expansion Model and Cosmology
- Extend the FRB model to include cosmological expansion effects (e.g., baryon content, dark matter, cosmological constant)
- Fit the combined FRB + redshift catalog with the cosmological model using MCMC
- Determine constraints on cosmological parameters and assess consistency with Planck data or other independent measurements
- Test Origin Hypotheses: Investigate whether FRB statistics distinguish between three population models
- NFRB∝ total stellar mass
- NFRB∝ star formation rate
- NFRB∝ presence of a central supermassive black hole
Deliverables:
- Code and Plots: well-documented code for MCMC modeling and plotting routines showing posterior distributions and parameter correlations
- Scientific Report: a concise LaTeX-written report summarizing data processing, assumptions, MCMC methodology, results, and conclusions
- Presentation: a 10-minute talk explaining the project, data used, model construction, parameter constraints, and interpretation of results
Project 3. TXS 0506–056 as a neutrino source. What can be derived from IceCube
and Baikal-GVD observations?
The Baikal-GVD Collaboration reported [MNRAS 527 (2023) 3, 8784–8792] neutrino events near the position of the blazar TXS 0506–056, a location previously associated with a high-energy neutrino observed by IceCube. This raises the question: is this spatial coincidence significant, and what does it reveal about the nature of the source?
Tasks:
- Build a Numerical Model
- Simulate neutrino events from both astrophysical background and source-related flux
- Include directional uncertainties and effective areas of IceCube and Baikal-GV
- Model the TXS 0506–056 neutrino flux under different scenarios (e.g. steady vs flaring activity, isotropic vs jet emission)
- Probability Space and Coincidence Analysis
- Define the probability space of “coincidences” in time and space between events in both detectors
- Calculate the chance probability of detecting spatially close neutrinos by both observatories
- Vary source model parameters to study how this affects the coincidence likelihood
- Inference on Source Properties
- Using the simulated distributions, assess which source models are compatible with the data
- Consider both steady emission and flaring activity
- Impact of Systematic Uncertainties
- Analyze how angular resolution, energy reconstruction, and background estimation errors affect the significance of the observed coincidence
- Quantify how much systematics weaken or strengthen conclusions about the source
Deliverables:
- Code and Plots: a working simulation with adjustable source parameters and outputs for event
- Scientific Report: a concise LaTeX-written report presenting the model, results, interpretation, and impact of uncertainties
- Presentation: a 10–15-minute talk summarizing the approach, findings, and implications for interpreting TXS~0506–056 as a neutrino source
Project 4. Muon and Electron Signatures in Super–Kamiokande and Sensitivity to Proton Decay
Muons and electrons are both charged leptons but exhibit very different behavior in detectors due to their mass and interaction processes. Super–Kamiokande (SK), a large water Cherenkov detector, is used to detect neutrinos and search for rare processes like proton decay. This project investigates the interaction and detection characteristics of muons and electrons and evaluates the sensitivity of SK to proton decay.
Analyze and compare the energy deposition mechanisms of muons and electrons, estimate particle ranges, and determine the limits of full containment in SK. Evaluate its sensitivity to proton decay assuming optimal detection conditions.
Tasks:
- Energy Deposition Differences
- Compare the energy loss mechanisms of e and μ in matter (ionization, bremsstrahlung, pair production)
- Explain qualitatively how this affects the topology of Cherenkov rings in water detectors
- Range Estimation in Matter
- Estimate the range of a 1~GeV e and μ in water and lead
- Use appropriate radiation length and energy loss formulae for rough numerical estimates
- Containment in SK
- Find the geometric size of the SK inner detector
- Estimate the maximum energy of a neutrino such that the entire final-state lepton remains within the detector volume (“fully contained event”)
- Proton Decay Signal: Analyze the expected signal for p → e+ + π0. Describe number and type of Cherenkov rings, kinematic features of the event, and background suppression strategy
- Proton Lifetime Sensitivity
- Assuming no background and perfect efficiency, what p lifetime lower bound that can be set by SK?
- Use the number of free protons in water and exposure time as parameters
Deliverables:
- Estimates and Plots: tables and simple plots showing range estimates, containment criteria, and the estimated proton lifetime constraints
- Scientific Report: a concise LaTeX-written report summarizing assumptions, estimates, and conclusions
- Presentation: a 10-minute talk presenting findings, estimates, and implications for neutrino physics and proton decay searches
Project 5. Production and Use of 18F for Neutrino Detector Calibration
Prof. Jianglai Liu discussed that certain n-activated radionuclides are
valuable for calibrating neutrino detectors. One such isotope is fluorine-18 (18F), a e+ emitter widely used in medical imaging and neutrino physics. In this project, you will design a method to produce 18F using a compact n-generator, analyze its decay signature, and study its application in calibrating a liquid scintillator detector (LSD), like JUNO.
Tasks:
- Design of the Activation Setup
- Use a D-T neutron generator (106 n s-1) to irradiate polytetrafluoroethylene (PTFE) containing 18F atoms
- Calculate the n capture cross-section and estimate the required irradiation time and PTFE mass to produce a 100 Bq of 18F source
- Decay Properties
- Describe the decay of 18F: type of decay, positron energy spectrum, and annihilation photons
- Include the half--life (~110 minutes) and its relevance for detector calibration
- Detector Response Modeling
- Assume the irradiated PTFE is sealed in a stainless-steel capsule and placed in the center of a large LSD
- Describe the expected energy spectrum from positron annihilation, and the visible energy from positron kinetic energy + 511 keV γγ-rays
- Energy Resolution: Given a photon yield of 1600 photoelectrons per MeV, estimate the statistical energy resolution for a typical 18F positron event. Comment on the detector effects (e.g., quenching) if applicable
- Calibration Precision
- Evaluate how precisely the detector energy scale can be calibrated using the annihilation peak
- Consider timing and data acquisition constraints related to the lifetime of 18F
Deliverables:
- Calculations and Plots: Neutron activation yield estimates, energy spectrum simulation or sketch, and energy resolution evaluation
- Scientific Report: a concise LaTeX-written report detailing the activation method, detector modeling, and expected calibration precision
- Presentation: a 10-minute talk summarizing the production method, detector signal, and implications for neutrino detector calibration
Project 6. Short-Baseline Reactor Neutrino Experiment for Sterile Neutrino Search
Sterile neutrinos are a hypothetical fourth generation of neutrinos that do not interact via the weak interaction. One way to search for them is through the disappearance of reactor antineutrinos at very short baselines. In this project, you will analyze the design and sensitivity of such an experiment located a few meters from a reactor core.
Design and analyze a short-baseline reactor neutrino experiment to search for a sterile neutrino with mass around 1 eV/c2, and estimate the experimental requirements to achieve sensitivity to a small mixing angle.
Tasks:
- Reactor Neutrino Energy
- Identify the typical energy spectrum of reactor antineutrinos
- Estimate the average energy relevant for inverse beta decay (IBD) detection
- Oscillation Baseline: For a sterile neutrino mass of 1 eV/c2, determine the optimal baseline L
- Detection Channel
- Describe the IBD process antiνe+p→ e++n
- Explain the experimental signature: prompt positron energy, delayed neutron capture
- Event Rate Estimate: Given antineutrino flux 2×1018 antiνe s-1, 1 ton of liquid scintillator (CH2) detector, 10-41 cm2 IBD cross-section, and assuming no oscillations, estimate the daily detection rate
- Precision on Mixing Angle: The mixing angle appears in the survival probability as follows: 1−0.5 sin2 θ14 ∝ NdetectedNexpected
- Determine how many events are needed to measure a 1% deviation in N/N0
- Estimate the required operation time (in days) to reach this precision, assuming statistical uncertainty dominates
Deliverables:
- Calculations and Plots: Oscillation pattern vs. distance, daily rate estimates, time vs precision curve
- Scientific Report: a concise LaTeX-written report report summarizing physical assumptions, calculations, and feasibility of sterile neutrino detection
- Presentation: a 10-minute talk explaining the experiment concept, key estimates, and sensitivity to small mixing angles
Project 7. Solar Neutrinos, Tritium Background, and Dark Matter in XENON1T
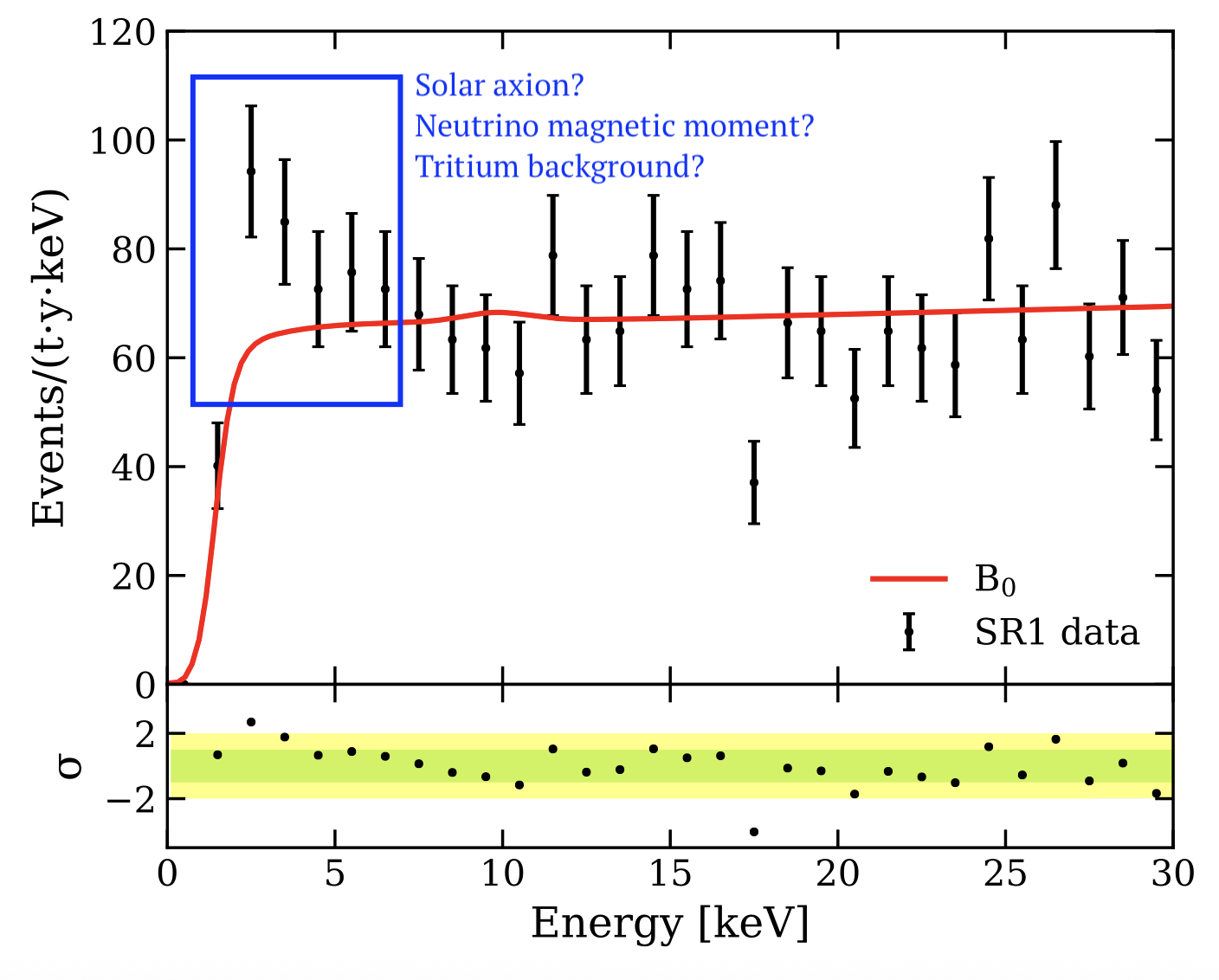
The XENON1T experiment is a liquid xenon detector designed primarily for dark matter (DM) searches, but it is also sensitive to neutrino interactions and low-energy backgrounds. In 2020, an excess of low-energy electron recoil events was reported, leading to discussions about possible new physics or background explanations. This project explores solar neutrino interactions, background estimation, and expected DM signals.
Estimate the number of expected neutrino and dark matter events in XENON1T, analyze the low-energy excess, and determine if it could be explained by a small amount of tritium contamination.
Tasks:
- Solar Neutrino Flux: Look up the flux and energy spectrum of 8B solar neutrinos. Define the relevant energy range for elastic scattering with electrons and Xe nuclei
- Neutrino Scattering Event Rates
- Estimate the number of events due to ν-e and ν-nucleus (coherent) scattering (using σscat from the lecture)
- Use the full exposure: 1.04 ton × 0.62 year, and assume zero threshold
- Expected Energy Spectra
- Sketch or simulate the differential energy spectra for both electron and nuclear recoils from solar neutrinos
- Discuss the spectral shape and relevant features (e.g., recoil energy range, endpoint)
- Tritium Hypothesis for Low-Energy Excess: Use the XENON1T data (electron recoil spectrum) showing a slight excess at low energies. Assuming it is due to 3H (τ1/2 = 12.3 years, Q=18 keV), estimate total number of 3H atoms in the detector (hint: observed event excess → decay rate → number of atoms)
- DM Signal Estimate: For DM of mass 100 GeV/c2, and cross section 10-42 cm2, assumming a standard local DM density and velocity, estimate the expected number of DM-Xe scattering events under the same exposure
Deliverables:
- Calculations and Plots: event rate estimates, recoil energy spectra, tritium background fit
- Scientific Report: a concise LaTeX-written report detailing neutrino and DM signal estimates, background analysis, and interpretation.
- Presentation: a 10-minute talk explaining the goals, methods, and key results related to neutrino detection, low-energy excess interpretation, and DM expectations
Project 8. Experimental Search for Neutrinoless Double Beta Decay in Liquid Xenon Detectors
Experimental search of neutrinoless double beta decay (0νDBD) requires extremely low background detectors, high energy resolution, and large target mass. Consider the 0νDBD of 136Xe (9% abundance in natural Xe) and the PandaX detector described in [Sci. China Phys. Mech. Astron. 68, 221011 (2025)].
Tasks:
- γ-background in such detectors is very difficult to shield. Explain qualitatively how γ-rays interact with Xe
- What observable features can be used to distinguish between γ-induced background and true 0νDBD signal?
- Using the baseline background level given in Table 3 of the article, and assuming an energy resolution of 1% at the Q-value of 2.46 MeV, estimate the lower limit on the 0νDBD lifetime that can be reached after 10 years of operation
- For a typical 0νDBD event, estimate the track length of the two electrons in liquid Xe
- Estimate the number of Cherenkov photons produced by the two β-particles in such an event
- Given the information from Parts (4) and (5), and assuming no cost constraints, propose additional experimental techniques or detector designs that could help uniquely identify 0νDBD events and suppress background
Deliverables:
- Analytical Estimates and Supporting Calculations
- Scientific Report: a concise LaTeX-written report summarizing your work.
- Presentation: a 10-minute talk summarizing your approach, results, and design suggestions
Project 9. Lunar-Based Ultimate Neutrino Telescope
Imagine the next generation of neutrino astronomy, unconstrained by Earth limitations. The Moon offers a stable, low-background, seismically quiet, and atmosphere-free environment ideal for deploying a revolutionary neutrino telescope. This project explores the conceptual design of a Moon-based detector optimized for detecting ultra-high-energy astrophysical neutrinos.
Propose a realistic design of a large-scale neutrino detector on the Moon. Engineer the detection concept, estimate performance, and formulate a scientific case for funding a space-based mission to observe the most energetic neutrinos in the Universe.
Tasks:
- Detector Concept and Lunar Deployment
- Propose a detection method (e.g., engineered lunar regolith, embedded scintillator/optical sensors, cryogenic detection media, or invent new one)
- Describe the layout, geometry, and location (e.g., permanently shadowed craters, regolith-shielded shafts)
- Address how to install or deploy the system robotically or with minimal human intervention
- Scientific Reach and Simulation
- Estimate energy range and sensitivity
- Calculate expected detection rates of ultra-high-energy neutrinos from astrophysical or cosmogenic sources
- Discuss angular resolution and sky coverage
- Technological Challenges and Solutions
- Identify challenges related to power, communication, cooling, shielding, and data handling on the Moon
- Propose solutions or identify existing technologies that could be adapted
- Visualization: Produce schematic plots or animations illustrating the layout and detection principle
- Budget and Proposal Defense
- Draft a simplified but credible funding request, including mission phases (design, transport, deployment, operations), rough cost estimates for major components, and justification of cost based on scientific return
- Prepare a short pitch: you are a collaboration seeking funding for a large-scale lunar neutrino telescope. Your job is to convince the funding committee that the investment is worth it.
Deliverables:
- Design Document and Plots: detector layout, simulation results, expected rates
- Scientific Report: a concise LaTeX-written report covering technical concept, scientific potential, and budget justification
- Presentation: a 10-minute talk presenting and explaining the mission concept as a funding proposal: why this telescope, why the Moon, and why now
Project 10. Can Earth’s Atmosphere Serve as the Largest Neutrino Detector?
While traditional neutrino detectors rely on dense media like water or ice to ensure sufficient interaction rates, the Earth’s atmosphere, despite its low density, covers a vast volume and area. From orbit, one can observe fluorescence or Cherenkov light from extensive air showers initiated by ultra-high-energy neutrinos or gamma rays. Additionally, the Earth itself can act as a shield, allowing only neutrinos to skim through and initiate detectable upward-going events.
Evaluate the viability of using Earth's atmosphere as a large-scale neutrino detector. Estimate interaction rates, compare with water-based detectors, and identify the energy regime where atmospheric detection becomes competitive. Propose a realistic orbital detection concept and defend it as a scientific mission.
Tasks:
- Atmosphere vs Water as Detection Medium
- Estimate the effective mass of the atmosphere available for detection (e.g., viewed from orbit)
- Compare the density and interaction probability with a 1 km3 water Cherenkov detector
- At what energies does the atmosphere become competitive or superior in detection power?
- Neutrino and Gamma Detection Modes
- Distinguish two primary modes: (1) down-going ν or γ-rays initiating air showers and (2) earth-skimming ντ producing upward-going air showers (τ decay in atmosphere)
- Describe the observational signature in each case (e.g., fluorescence track, Cherenkov flash)
- Rate Estimates
- For given ultra-high-energy neutrino flux models, estimate the expected number of events per year visible from space using a reasonable field of view
- Compare to expected rates in IceCube or other large-scale detectors
- Mission Design: Propose a detection system (e.g., EUSO-like orbital platform with optical detectors). Specify detection principle, coverage area, expected sensitivity, and background suppression strategiese
- Budget and Proposal Defense: Outline the mission phases: design, construction, launch, operation. Provide rough cost estimates. Prepare a short pitch defending your proposal: why observe from space, why use the atmosphere, and why it is worth the investment
Deliverables:
- Estimates and Visuals: comparative calculations and schematic plots demonstrating detection concept
- Scientific Report: a concise LaTeX-written report including estimates, physics justification, and budget outline
- Presentation: a 10-minute talk presenting the mission concept and scientific case as a funding proposal
